

Recent research has shown that it is possible to find interpretable directions in the latent spaces of pre-trained GANs. These directions enable controllable generation and support a variety of semantic editing operations such as zoom-in or rotation. While existing work focuses on discovering directions for semantic image editing, limited work has been done on manipulating cognitive properties such as memorability or emotional valence. In this paper, we propose a novel framework that discovers multiple directions to manipulate cognitive properties. We show that our framework provides better manipulation for images with cognitive properties such as Emotional Valence, Memorability and Aesthetics.
There is very little work on discovering interpretable directions for cognitive properties such as memorability, emotional valence, and aesthetics. Compared to traditional semantic directions such as zoom, shift, or rotation, cognitive properties do not have an exact definition of what they mean. For example, while we can write editing functions to perform zoom-in or transformation operations on the image, we do not have a concrete definition of what memorability is. In this work, we propose a novel framework for discovering latent directions for cognitive features to learn multiple directions. We apply our method to cognitive features such as emotional valence, memorability and aesthetics. Our quantitative and qualitative experiments show that our method outperforms previous methods and provides better manipulations on cognitive features.
In this work, we use a pre-trained GAN model with a generator G. G is a mapping function that takes a noise vector z ∈ R of dimension d and a one-hot class vector y ∈ {0,1} of size 1000 as input and generates an image G(z,y) as output. The latent code z is drawn from a prior distribution p(z), typically chosen to be a Gaussian distribution. We also assume that we have access to a scorer function S that returns a score that evaluates the property of interest, and a is a scalar value representing the degree of manipulation we wish to achieve. Our goal is to find k diverse directions n_1, n_2, ... n_k that minimize the following optimization problem: $$\mathbf{N}^* = argmin{\{\mathbf{N} \in \mathbb{R}^{d\times k}\}} \sum_{i=1}^k \mathcal{L}_{i} + \lambda \mathcal{L}_{div}$$ N = [n_1, n_2, ... n_k] corresponds to the k directions learned from our model, L_i is the conditional loss, which is computed based on the input and the direction i, and L_div is the regularization loss term that penalizes directions that are similar to each other. λ is a hyperparameter that balances the manipulability and diversity of the learned directions. L_i is defined as: \begin{equation} \mathcal{L}_{i} = \mathbb{E}_{\mathbf{z},\mathbf{y},\alpha} [ (S(G(F_i(\mathbf{z}, \alpha), \mathbf{y})) - (S(G(\mathbf{z}, \mathbf{y})) + \alpha))^2 ] %S(G(T(z, α), y)) − (A(G(z, y)) + α))2 \end{equation} where the first term represents the score of the modified image after applying the conditional edit function F_i given parameters z and a, and the second term simply represents the score of the original image S(G(z,y)) increased or decreased by a. F_i computes a conditional direction n_i using a neural network of two dense layers with a RELU nonlinearity in-between. $$F_i(\mathbf{z}, \alpha) = \mathbf{z} + \alpha \cdot \mathbf{NN}_i(\mathbf{z}).$$ L_div acts as a regularizer and penalizes the directions that are similar to each other. We define L_div as follows: \begin{equation} \mathcal{L}_{div} = \sum_{i,j, i\neq j}^{k} \mathbf{F_{sim}} (\mathbf{n_i}, \mathbf{n_j}) \end{equation} where F_sim simply computes the similarity between vectors n_i and n_j. In this work, we use the cosine similarity as a metric however any metric that measures the similarity between two vectors can be easily fitted.
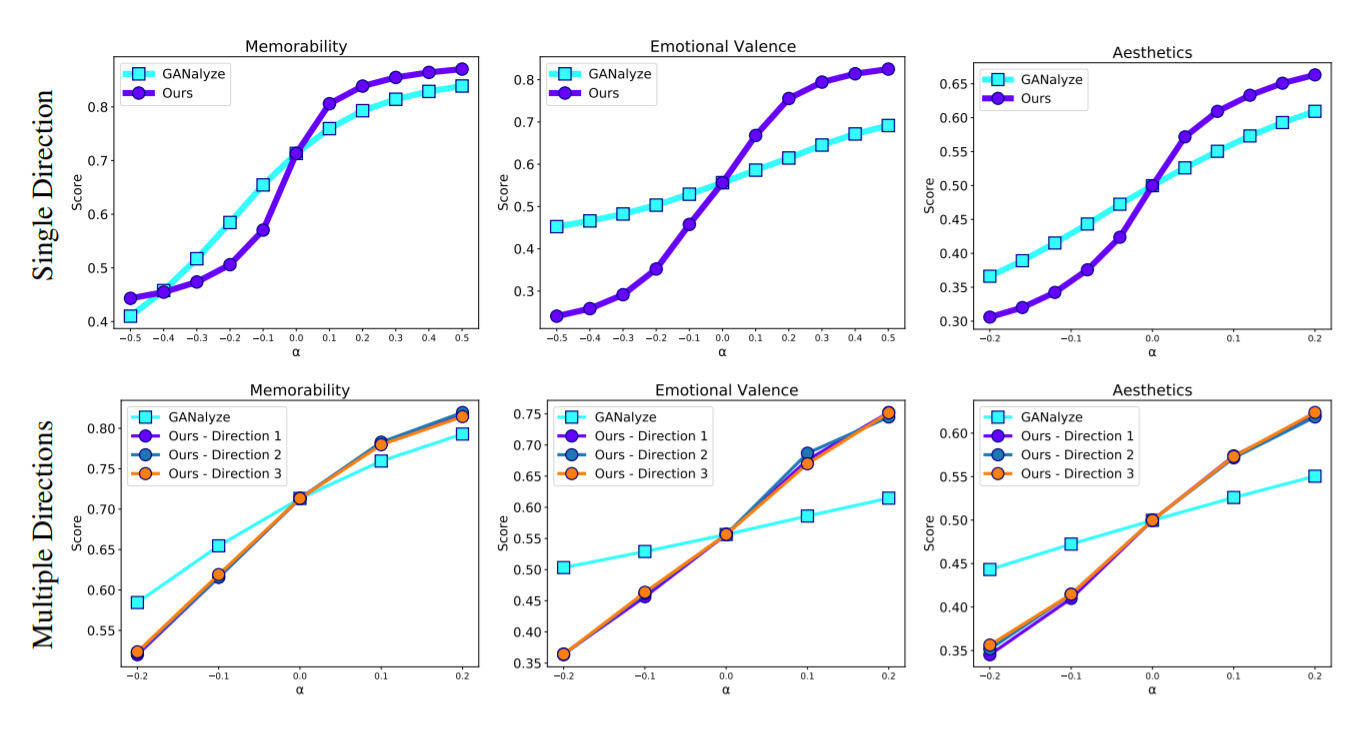
We first investigate whether our model learns to navigate the latent space in such a way that it can increase or decrease the desired property by a given α value. As can be seen from Figure 1, our model performs better than GANalyze.
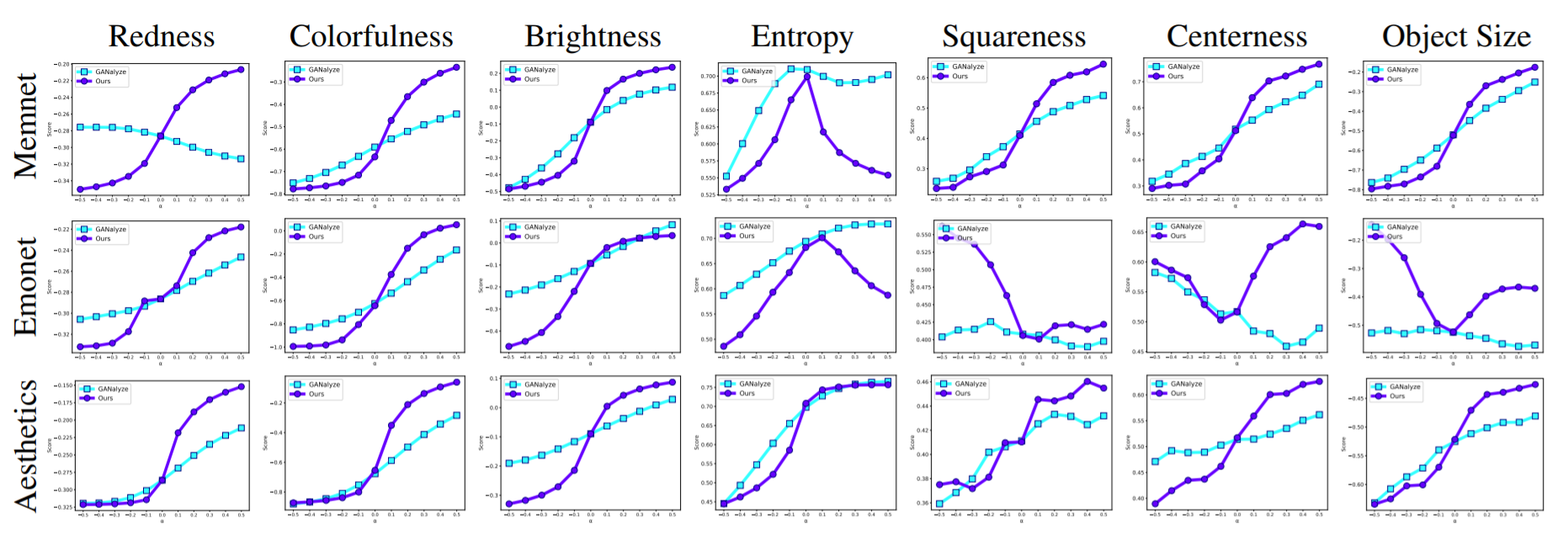
Next, we investigate what kind of image factors are changed to achieve these improvements. We examined redness, colorfulness, brightness, simplicity, squareness, centeredness and object size as can be seen from Figure 2.
Our visual results for single direction can be found in Figure 3.

Our visual results for multiple directions can be found in Figure 4.

In this study, we propose a framework that learns diverse manipulation for cognitive properties. We applied it to memorability, emotional valence, Aesthetics and show that our method makes a better manipulation than GANalyze while producing diverse outputs. We also investigated which visual features contribute to achieving certain manipulations.
@article{kocasari2022latentcognitive,
author = {Kocasari, Umut and Bag, Alperen and Yüksel, Oğuz Kaan and Yanardag, Pinar},
title = {Discovering Diverse Directions for Cognitive Image Properties},
journal = {arxiv},
year = {2022},
}