Fantastic Style Channels and Where to Find Them:
A Submodular Framework for Discovering Diverse Directions in GANs

Enis Simsar1, Umut Kocasarı2, Ezgi Gulperi Er2, Pınar Yanardağ2
1TUM, 2Bogazici University
arXiv Code StyleAtlas

Abstract

The discovery of interpretable directions in the latent spaces of pre-trained GAN models has recently become a popular topic. In particular, StyleGAN2 has enabled various image generation and manipulation tasks due to its rich and disentangled latent spaces. The discovery of such directions is typically done either in a supervised manner, which requires annotated data for each desired manipulation, or in an unsupervised manner, which requires a manual effort to identify the directions. As a result, existing work typically finds only a handful of directions in which controllable edits can be made. In this paper, we attempt to find the most representative and diverse subset of directions in stylespace of StyleGAN2. We formulate the problem as a coverage of stylespace and propose a novel submodular optimization framework that can be solved efficiently with a greedy optimization scheme. We evaluate our framework with qualitative and quantitative experiments and show that our method finds more diverse and relevant channels.

Italian Trulli
Figure 1: Our submodular framework uses the notion of clusters to select the most representative and diverse set of style channels. Channels performing similar or different manipulations are shown in clusters above. The input images are displayed in the first column.

Methodology

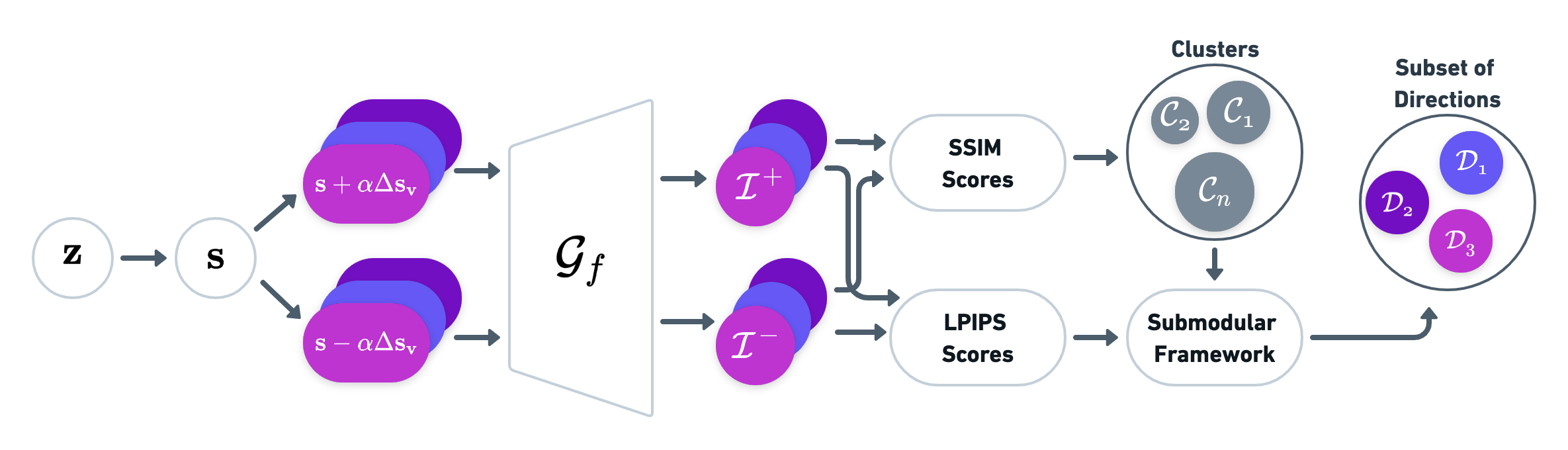
Italian Trulli
Figure 2: We randomly sample $M$ latent vectors $\mathbf{z} \in \mathcal{Z}$, which are transformed into style vectors $\mathbf{s}$. An arbitrary channel $v$ in $\mathcal{S}$ are perturbed by a certain amount $\alpha$ in positive and negative directions such that $(\mathbf{s}+\alpha\Delta\mathbf{s_v})$ and $(\mathbf{s}-\alpha\Delta\mathbf{s_v})$, where $\Delta\mathbf{s_v}$ is a vector containing all zeros except one of its dimensions, which is equal to one for channel $v$. LPIPS and SSIM scores are computed for the images obtained from the perturbed vectors, which are then used to generate clusters and select channels using the submodular framework.


Let $\mathcal{V}$ represent the set of style channels in the stylespace. Then, we are interested in selecting a small subset of channels $\mathcal{P} \subseteq \mathcal{V}$ that are most representative and diverse. To measure the overall coverage or fidelity of the channels in $\mathcal{P}$, we can define a set function as follows, \begin{equation} \mathcal{F}_{coverage}(\mathcal{P}) = \sum_{v_i \in \mathcal{V}, v_j \in \mathcal{P}} \mathcal{F}_{\text{sim}}(v_i, v_j) \label{eq:coverage} \end{equation} which simply computes the similarity between the summary set $\mathcal{P}$ and the ground set $\mathcal{V}$. In other words, it measures some form of coverage of $\mathcal{V}$ by $\mathcal{P}$. $\mathcal{F}_{\text{sim}}$ measures the similarity between two channels using SSIM metric. However, this function does not take diversity into account, since the value of the covering a particular type of edit (such as hair or background) never diminishes. A common approach is to apply a diversity regularization to our objective function [1], where we aim to reward items selected from different groups of directions such that: \begin{equation} \mathcal{F}_{diversity}(\mathcal{P}) = \log \left( 1 + \sum_{k=1}^K \left( \sum_{v_i \in \mathcal{C}_k \cap \mathcal{P}} \mathcal{F}_{\text{reward}}({v_i}) \right) \right) \label{eq:diversity} \end{equation} where the ground set $\mathcal{V}$ of style channels is partitioned into $K$ separate clusters. The clusters $\mathcal{C}_k$ are disjoint, where $k=1, \ldots K$ and $\bigcup_k \mathcal{C}_k = \mathcal{V}$. For each style channel $v_i$, we have a reward $\mathcal{F}_{\text{reward}}({v_i}) \geq 0$, which indicates the importance of adding channel $v_i$ to the empty set which is computed using LPIPS metric. Then, the overall objective function we want to solve is a combination of both: \begin{equation} \mathcal{F}(\mathcal{P}) = \mathcal{F}_{coverage}(\mathcal{P}) + \lambda \mathcal{F}_{diversity}(\mathcal{P}) \label{eq:submod_channels} \end{equation} where $\lambda \geq 0$ is the tradeoff coefficient between coverage and diversity. Since we are interested in selecting a small subset, we aim to maximize the following objective function, \begin{equation} \mathcal{P}^* = argmax_{\mathcal{P} \subseteq \mathcal{V}: |\mathcal{P}| \leq n} \mathcal{F}(\mathcal{P}) \label{eq:argmax} \end{equation} subject to a cardinality constraint $n$, which denotes the total number of channels in the set $\mathcal{P}^*$. This objective function combines two aspects in which we are interested: 1) it encourages the selected set to be representative of the stylespace, and 2) it positively rewards diversity. Finding the exact subset that maximizes this equation is intractable. However, it has been shown that maximizing a monotone submodular function under a cardinality constraint can be solved near optimally using a greedy algorithm [2]. In particular, if a function $\mathcal{F}$ is submodular, monotone and takes only non-negative values, then a greedy algorithm approximates the optimal solution of this equation within a factor of $(1 - 1/e) $ [2].

Experiments

Clustering Stylespace Our submodular framework relies on the clusters to encourage diversity. Clusters from the FFHQ, Fashion, AFHQ Cats, LSUN Cars, and Metfaces datasets are shown below. We note that clusters that modify similar regions are grouped together, such as smile, hairstyle, expression in FFHQ, neck type, color, pattern in Fashion, eye color, eye, ear type in AFHQ Cats, roof type, ground, bumper type in LSUN Cars, eyebrow type, hairsyle, expression in Metfaces.


Italian Trulli
Figure 3: Various clusters on FFHQ, Fashion, AFHQ Cats, LSUN Cars, Metfaces datasets. Three different clusters are shown for each dataset, with the first column representing the input image and the remaining columns showing the manipulation performed by a random channel in the cluster.


Covering stylespace Figure 6 shows the top 10 channels ranked by our method considering multiple layers. As can be seen from the results, our method selects a variety of channels that modify regions such as background, hair, face, mouth, eye, ear, and clothing. Our method yields more disentangled and diverse directions compared to Ganspace and SeFa. For example, while both Ganspace and SeFa change semantics in the input, such as gender, age, eyeglasses, while also changing other semantics such as background, position, highlight at the same time. In contrast, our method performs disentangled edits by changing one semantic at a time.


Italian Trulli
Figure 6: Comparison of top-10 directions for Ganspace, SeFa, and our method. First column shows the original image.

Applications

Our framework also opens up possibilities for interesting applications that help users discover new directions.

Interactive Editing Users can navigate the stylespace by drawing a region of interest such as hair and retrieving relevant clusters and corresponding channels.


Italian Trulli
Figure 8: Filtered clusters based on a region specified by the user. The two images in the upper left show the input image and the region specified by the user, while the other images show a sample manipulation performed with a randomly selected channel from each retrieved cluster

Exploration Platform We also provide a web-based platform called StyleAtlas at https://catlab-team.github.io/styleatlas where users can explore the stylespace in a fine-grained way. This tool allows users to explore the manipulations made by specific channels based on the region and discover style channels of interest.


Italian Trulli
Figure 9: A view of the stylespace exploration platform where each group represents a different region, such as. nose or eyes. The bubbles represent manipulation done by a particular channel. The full version is omitted for anonymity purposes. The colors around the bubbles represent different layers (zoom for better view).

Conclusion

In this work, we consider the selection of diverse directions in the latent space of StyleGAN2 as a coverage problem. We formulate our framework as a submodular optimization for which we provide an efficient solution. Moreover, we provide a complete guide to the stylespace in which one can explore hundreds of diverse directions formed by style channels using clusters. In our experiments, we have shown that our method can identify a variety of manipulations, and performs diverse and disentangled edits.

Acknowledgements

This publication has been produced benefiting from the 2232 International Fellowship for Outstanding Researchers Program of TUBITAK (Project No:118c321).

References

[1] Lin, H., & Bilmes, J. (2011, June). A class of submodular functions for document summarization. In Proceedings of the 49th annual meeting of the association for computational linguistics: human language technologies (pp. 510-520).
[2] Nemhauser, G. L., Wolsey, L. A., & Fisher, M. L. (1978). An analysis of approximations for maximizing submodular set functions—I. Mathematical programming, 14(1), 265-294.